Rumus Segitiga Sama Sisi Dan Pythagoras Segitiga
Segitiga sama sisi yakni jenis segitiga yang ketiga sisi mempunyai ukuran yang sama panjang. Karena sisinya yang sama panjang, setiap titik sudut pada segitiga sama sisi mempunyai besar 60°. Rumus segitiga sama sisi mempunyai formula yang istimewa, yang merupakan aplikasi dari teorema Pythagoras.
Baca juga: Jenis Segitiga, Rumus Luas dan Keliling Segitiga
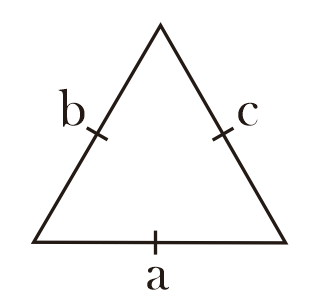
a, b, c = sisi segitiga
| Nama | Rumus |
| Luas (L) | L = ½ × a × t |
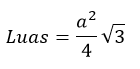 | |
| Keliling (Kll) | Kll = sisi a + sisi b + sisi c |
| Kll = 3 × panjang sisi | |
| Sisi atau Alas (a) | Sisi = Keliling ÷ 3 |
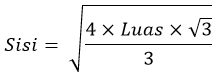 | |
| Tinggi (t) | t = (2 × Luas) ÷ a |
 |
Catatan: Contoh soal disediakan di bab bawah
A. Karakteristik Segitiga Sama Sisi
Berikut sifat-sifat segitiga sama sisi,
-
Ketiga sisinya mempunyai panjang yang sama.
Pada segitiga sama sisi berlaku panjang sisi a = b = c.
-
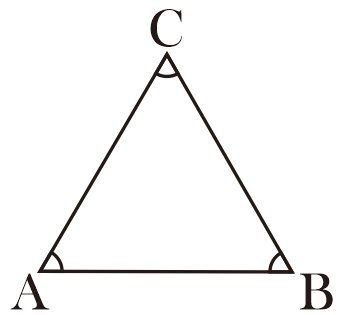
Ketiga titik sudutnya berukuran 60°.
Pada segitiga sama sisi berlaku ∠ABC = ∠BCA = ∠CAB = 60º. Hal ini terjadi alasannya yakni jumlah total sudut segitiga yakni 180º.
-
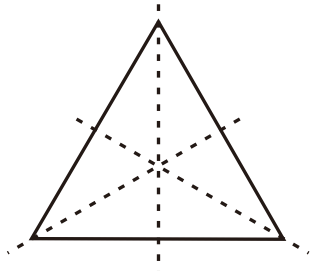
Mempunyai 3 sumbu simetri.
Segitiga mempunyai 3 sumbu simetri yang masing-masing sanggup membagi segitiga menjadi pasangan berdiri datar yang simetris.
-
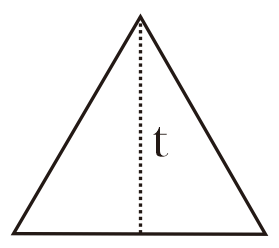
Sumbu simetri sanggup dipakai sebagai tinggi segitiga.
Tinggi segitiga yakni sekaligus sumbu simetrinya, tinggi segitiga sama sisinya sanggup membagi segitiga sama sisi menjadi pasangan berdiri yang simetris.
B. Rumus Luas dan Keliling Segitiga Sama Sisi
| Nama | Rumus |
| Luas (L) | L = ½ × a × t |
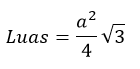 | |
| Keliling (Kll) | Kll = sisi a + sisi b + sisi c |
| Kll = 3 × panjang sisi | |
| Sisi atau Alas (a) | Sisi = Keliling ÷ 3 |
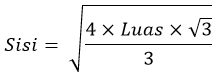 | |
| Tinggi (t) | t = (2 × Luas) ÷ a |
 |
B.1 Rumus Luas Segitiga Sama Sisi
Terdapat 2 cara menghitung luas segitiga sama sisi, yaitu:
Luas = ½ × a × t
Luas segitiga sama sisi hanya diketahui panjang sisi
Luas = (a² ÷ 4) × √3
atau
Dengan a = ganjal dan t = tinggi
Contoh 1:
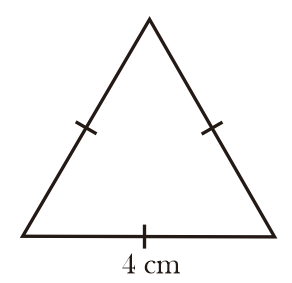
Hitunglah luas segitiga sama sisi pada gambar berikut!
Diketahui:
panjang sisi 4 cm
Ditanya:
Luas!
Penyelesaian:
Luas = (a² ÷ 4) × √3
Luas = (4² ÷ 4) × √3
Luas = (16 ÷ 4) × √3
Luas = 4√3 cm²
Jadi, luas segitiga sama sisi tersebut yakni 4√3 cm²
B.2 Rumus Keliling Segitiga Sama Sisi
Secara umum keliling suatu segitiga adalah
Keliling = sisi a + sisi b + sisi c
Karena segitiga sama sisi mempunyai tiga sisi yang sama panjang, formula tersebut sanggup disederhanakan lagi,
Keliling = 3 × Panjang sisi
Sehingga formula tersebut sanggup menghasilkan panjang sisi segitiga sama sisi,
Panjang sisi = Keliling ÷ 3
C. Rumus Tinggi Segitiga Sama Sisi dan Pendekatan Pythagoras
Tinggi segitiga sama sisi sanggup diperoleh dari pendekatan Pythagoras,
Baca juga: Rumus Pythagoras Segitiga dan Contoh Soalnya
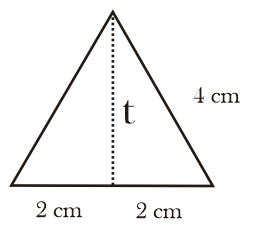
Pada gambar berikut diberikan segitiga sama sisi dengan panjang sisinya 4 cm. Dapat dibuat garis tinggi yang merupakan sumbu simetri dari segitiga sama sisi, sehingga membagi ganjal menjadi 2.
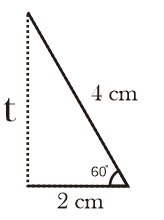
Kemudian kita sanggup mengambil lipatan yang dibuat sumbu simetri diatas,
Cara 1:
Dari sini kita sanggup dengan gampang mencari tinggi segitiga dengan memakai rumus trigonometri,
Sehingga sanggup dibuat rumus tinggi segitiga sama sisi adalah
Cara 2:
Dengan memakai pendekatan Pythagoras akan menghasilkan nilai yang sama
Baca juga tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel Rumus Segitiga Sama Sisi dan Pythagoras Segitiga Sama Sisi. Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai Fans Page Advernesia. Terima kasih…
Sumber https://www.advernesia.com/

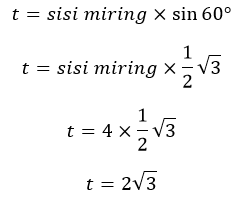
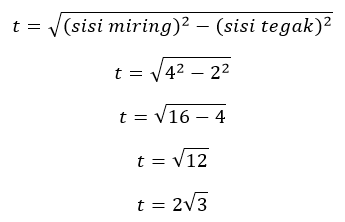

0 Response to "Rumus Segitiga Sama Sisi Dan Pythagoras Segitiga"
Posting Komentar