Pengertian Bilangan Prima, Rumus, Dan Pola Bilangan Prima 1-1000
A. Pengertian Bilangan Prima
Bilangan prima ialah bilangan orisinil yang bernilai lebih dari 1 dan mempunyai 2 faktor pembagi yaitu 1 dan bilangan itu sendiri. Bilangan prima mempunyai 2 faktor, berarti bilangan itu hanya habis dibagi oleh angka 1 dan bilangan itu sendiri.
Artikel terkait: Pengertian Bilangan Asli Beserta Contohnya
Contoh: 2 ialah bilangan prima
Penjelasan: Angka 2 hanya sanggup dibagi oleh angka 1 dan 2
Contoh bilangan Prima 1-100
Terdapat 25 bilangan prima antara 1-100
| 2 | 3 | 5 | 6 | 11 |
| 13 | 17 | 19 | 23 | 29 |
| 31 | 37 | 41 | 43 | 47 |
| 53 | 59 | 61 | 67 | 71 |
| 73 | 79 | 83 | 89 | 97 |
Catatan: Bilangan Prima 1-1000 di serpihan bawah.
Angka 2 ialah satu-satunya bilangan prima genap.
Pembuktian matematika “Tidak ada bilangan prima terbesar”
Untuk setiap bilangan prima p, terdapat bilangan prima p ‘seperti p’ lebih besar dari p. Bukti matematis ini, yang ditunjukkan pada zaman kuno oleh matematikawan Yunani Euclid, memvalidasi konsep bahwa tidak ada bilangan prima “terbesar”.
Kebalikan dari bilangan prima ialah bilangan komposit, yaitu bilangan orisinil bernilai lebih dari 1 serta mempunyai lebih dari 2 faktor pembagi.
Artikel terkait: Pengertian Bilangan Komposit beserta Contohnya
B. Contoh Bilangan Prima 1-1000
Terdapat 168 bilangan prima di antara angka 1-1000
1 bukanlah bilangan prima sebab 1 hanya mempunyai 1 faktor, sehingga bilangan prima dimulai dari angka 2.
2 merupakan satu-satunya angka prima genap, tidak terdapat bilangan prima lainnya yang bernilai genap.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997
C. Rumus Bilangan Prima | Cara Menentukan Bilangan Prima
Untuk menciptakan bilangan prima secara terurut, kita tidak perlu menghafalnya. Berikut algoritma bilangan prima
- Mulai
- Tulis 2 bilangan prima terkecil (2, 3)
- Lakukan langkah berikut sampai batas atas bilangan prima yang dicari
- Definisikan 2 bilangan prima berikutnya yaitu a (5) dan b (7)
- Jumlahkan a dengan angka 6, x = a + 6
- Jika x habis dibagi 5, maka x bukan prima
- Jika x tidak habis dibagi 5, x bilangan prima berikutnya
- Jumlahkan b dengan angka 6, y = b + 6
- Jika y habis dibagi 5, maka y bukan prima
- Jika y tidak habis dibagi 5, y bilangan prima berikutnya
- Ulang langkah 1, 2, 3 dengan mengubah nilai a = x dan b = y
- Selesai
Berikut ilustrasinya:
Misalnya akan dicari bilangan prima 1-40
Jadi, bilangan prima di antara 1-40 ialah 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37
D. Pengertian Faktor Prima dan Pohon Faktor
Faktor prima ialah bilangan-bilangan prima penyusun suatu bilangan komposit. Untuk mencari faktor prima suatu bilangan sanggup memakai pemberian pohon faktor.
Cara mencari faktor prima suatu bilangan memakai pohon faktor ialah dengan membagi bilangan secara terus menerus dengan bilangan prima terkecil yang mungkin.
Contoh:
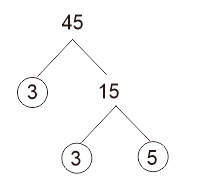
Carilah faktor prima dari 45?
Jadi, faktor prima dari 45 ialah 3 × 3 × 5
E. Kegunaan Bilangan Prima
- Dalam ilmu matematika bilangan prima dekat kaitannya dengan tingkat pembelajaran yang lebih tinggi, menyerupai mencari FPB, menyederhanakan pecahan, dan lain-lain.
- Bilangan prima dipakai dalam ilmu kriptografi (criptography) untuk melaksanakan enskripsi data. Aplikasinya memegang peranan yang penting terkait keamanan data, menyerupai network security, sistem keamanan rekening bank, dan lain-lain.
Baca juga tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel Pengertian Bilangan Prima. Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai Fans Page Advernesia. Terima kasih…



0 Response to "Pengertian Bilangan Prima, Rumus, Dan Pola Bilangan Prima 1-1000"
Posting Komentar