Rumus Berdiri Datar, Pengertian, Jenis, Dan Contohnya
A. Pengertian Bangun Datar (Plane Geometry)
Bangun datar yakni suatu bidang datar yang tersusun oleh titik atau garis-garis yang menyatu membentuk bangkit 2 dimensi yang memiliki keliling dan luas. Bangun datar merupakan sebuah aksioma di bidang ilmu matematika khususnya geometri analitik, alasannya hal ini sanggup terbukti dengan sendirinya tanpa melaksanakan pembuktian matematika lebih lanjut [H.S.M. Coxeter, “Introduction to geometry“, Wiley (1969) pp. 178]. Dalam bahasa inggris bangkit datar disebut dengan plane geometry. Berikut dijelaskan jenis-jenis dan rumus bangkit datar pada bab selanjutnya.
B. Jenis dan Rumus Bangun Datar beserta Contohnya
Berikut jenis-jenis dan rumus bangkit datar yang umum dipakai dalam pembelajaran matematika, untuk pola sanggup membuka tautan yang telah disediakan pada 8 jenis bangkit yaitu: segitiga, persegi, persegi panjang, jajar genjang, belah ketupat, layang-layang, trapesium, dan lingkaran.
1. Segitiga
Segitiga yakni bangkit datar yang terdiri dari 3 sisi garis lurus dengan 3 titik sudut yang berjumlah 180º.
Keterangan:
a = alas
t = tinggi, tinggi segitiga membentuk sudut 90° terhadap alasnya.
b, c = yakni sisi lain segitiga
| Nama | Rumus |
|---|---|
| Luas (L) | L = ½ × a × t |
| Keliling (Kll) | Kll = a + b + c |
| Tinggi (t) | t = (2 × Luas) ÷ a |
| Alas (a) | a = (2 × Luas) ÷ t |
Artikel terkait: Contoh Soal Segitiga
2. Persegi
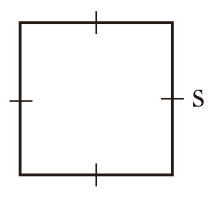
Persegi yakni bangkit datar 2 dimensi yang dibuat oleh empat sisi yang sama panjang dan keempat titik sudutnya membentuk sudut siku-siku (90º).
s = sisi persegi
| Nama | Rumus |
| Luas (L) | L = s × s |
| Keliling (Kll) | Kll = 4 × s |
| Sisi (s) | s = √L |
| s = Kll ÷ 4 | |
| Diagonal (d) |
Artikel terkait: Contoh Soal Persegi
3. Persegi Panjang
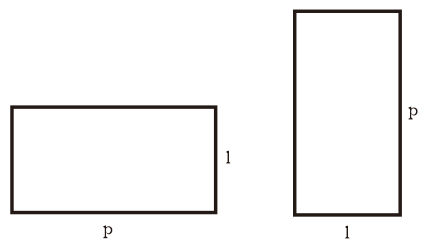
Persegi Panjang yakni bangkit datar 2 dimensi yang memiliki 2 pasang sisi sejajar yang sama Panjang dan memiliki 4 titik sudut siku-siku.
p = panjang, l = lebar
| Nama | Rumus |
| Luas (L) | L = p × l |
| Keliling (Kll) | Kll = 2 × (p + l) |
| Panjang (p) | p = L ÷ l |
| p = (Kll ÷ 2) – l | |
| Lebar (l) | l = L ÷ p |
| l = (Kll ÷ 2) – p | |
| Diagonal (d) |
Artikel terkait: Contoh Soal Persegi Panjang
4. Jajar Genjang
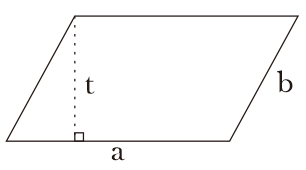
Jajar genjang yakni bangkit datar 2 dimensi yang tersusun oleh 2 pasang sisi yang sama panjang dan sejajar serta memiliki 2 pasang sudut yang sama besar (pasangan sudut lancip dan pasangan sudut tumpul).
a = sisi alas, b = sisi miring, dan t = tinggi
| Nama | Rumus |
| Keliling (Kll) | Kll = 2 × (a + b) |
| Luas (L) | L = a × t |
| Sisi Alas (a) | a = (Kll ÷ 2) – b |
| Sisi Sisi Miring (b) | a = (Kll ÷ 2) – a |
| t diketahui L | t = L ÷ a |
| a diketahui L | a = L ÷ t |
Artikel terkait: Contoh Soal Jajar Genjang
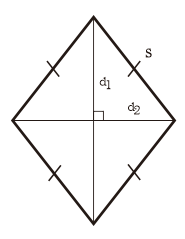
5. Belah Ketupat
Belah Ketupat yakni bangkit datar 2 dimensi yang dibuat oleh 4 buah sisi yang sama panjang dan memiliki 2 pasang sudut bukan siku-siku dengan sudut yang saling berhadapan memiliki besar sama.
| Nama | Rumus |
| Keliling (Kll) | Kll = s + s + s + s |
| Kll = s × 4 | |
| Luas (L) | L = ½ × d1 × d2 |
| Sisi (s) | s = Kll ÷ 4 |
| Diagonal 1 (d1) | d1 = 2 × L ÷ d2 |
| Diagonal 2 (d2) | d2 = 2 × L ÷ d1 |
Artikel terkait: Contoh Soal Belah Ketupat
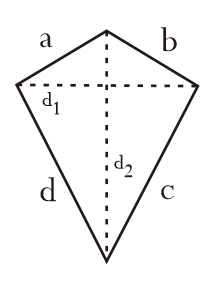
6. Layang-Layang
Layang-layang yakni bangkit datar yang dibuat oleh 2 pasang sisi sama panjang yang saling membentuk sudut yang berbeda.
| Nama | Rumus |
| Luas (L) | L = ½ × d1 × d2 |
| Keliling (Kll) | Kll = a + b + c + d |
| Kll = 2 × (a + c) | |
| Diagonal 1 (d1) | d1 = 2 × L ÷ d2 |
| Diagonal 2 (d2) | d2 = 2 × L ÷ d1 |
| a atau b | a = (½ × Kll) – c |
| c atau d | c = (½ × Kll) – a |
Artikel terkait: Contoh Soal Layang-Layang
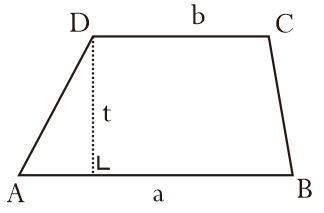
7. Trapesium
Trapesium yakni bangkit datar dua dimensi yang tersusun oleh 4 buah sisi yaitu 2 buah sisi sejajar yang tidak sama panjang dan 2 buah sisi lainnya.
t = tinggi trapesium
a, b = yakni sisi yang sejajar, sisi a merupakan panjang AB dan sisi b merupakan panjang DC
Artikel terkait: Contoh Soal Trapesium
8. Lingkaran
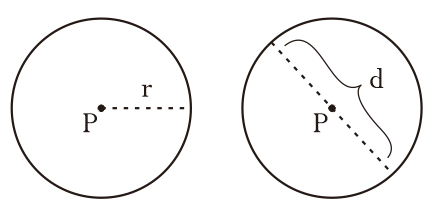
Lingkaran yakni bangkit datar dua dimensi dibuat oleh himpunan semua titik yang memiliki jarak sama dari suatu titik tetap.
| Nama | Rumus |
| Diameter (d) | d = 2 × r |
| Jari-jari (r) | r = d ÷ 2 |
| Luas (L) | 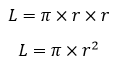 |
| Keliling (Kll) | 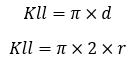 |
| Mencari r | 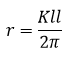 |
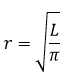 |
Artikel terkait: Contoh Soal Lingkaran
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel “Bangun Datar | Pengertian, Jenis, Rumus Bangun Datar dan Contohnya”. Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih…
Sumber https://www.advernesia.com/
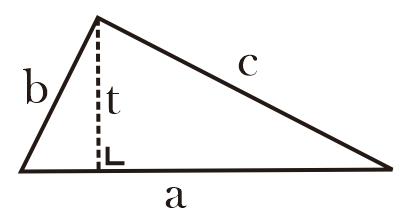
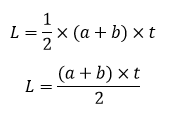
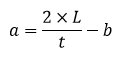
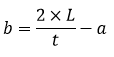
0 Response to "Rumus Berdiri Datar, Pengertian, Jenis, Dan Contohnya"
Posting Komentar